Archimedes Biograafia, panused ja leiutised
Arhimese Siracusa (287 a.C - 212 a.C) oli matemaatik, füüsik, leiutaja, insener ja kreeka astronoom Sitsiilia saarel asuvas iidses Syracuse linnas. Tema kõige silmapaistvamad panused on Archimedese põhimõte, väljumismeetodi väljatöötamine, mehaaniline meetod või esimese planetaariumi loomine..
Praegu peetakse seda Euklide ja Apolonio kõrval olevaks üheks antiikaja matemaatika kolmest olulisemast numbrist, kuna selle panus tähendas ajaloos olulisi teaduslikke edusamme arvutuse, füüsika, geomeetria ja astronoomia valdkonnas. See omakorda muudab temast ühe inimkonna ajaloo kõige silmapaistvamaid teadlasi.

Kuigi on teada vähe oma isikliku elu üksikasju - ja need, mis on teadaolevad, on kahtlase usaldusväärsusega, on tema panused teada tänu kirjalikele kirjadele tema teoste ja saavutuste kohta, mis on säilinud tänapäevani, kuuludes siiani. kirjavahetusele, mida ta aastaid sõprade ja teiste matemaatikutega hoidis.
Archimedes oli oma ajastul tuntud tänu oma leiutistele, mis tõmbasid tähelepanu oma kaaslastele, osaliselt seetõttu, et neid kasutati sõjaseadmetena, et edukalt vältida mitmeid Rooma sissetunge..
Siiski öeldakse, et ta väitis, et ainus tõesti oluline asi oli matemaatika ja et tema leiutised olid vaid rakendatud geomeetria ajaviide. Pärast järeltulemusi on tema teosed puhta matemaatika alal olnud palju kõrgemad kui tema leiutised.
Indeks
- 1 Biograafia
- 1.1 Koolitus
- 1.2 Teadustöö
- 1.3 Konflikt Siracuses
- 1.4 Surm
- 2 Archimedese teaduslik panus
- 2.1 Archimedese põhimõte
- 2.2 Mehaaniline meetod
- 2.3 Kangi õiguse selgitus
- 2.4 Uurimis- või ammendamismeetodi väljatöötamine teaduslikuks demonstratsiooniks
- 2.5 Ringi mõõt
- 2.6 Sfääride ja silindrite geomeetria
- 3 Leiutised
- 3.1 Odomeeter
- 3.2 Esimene planetaarium
- 3.3 Archimedese kruvi
- 3.4 Archimedese küünis
- 4 Viited
Biograafia
Syracuse Archimedes sündis umbes eKr 287. aastal. Tema varasemate aastate kohta pole teada palju, kuigi võib öelda, et ta on sündinud Syracuse linnas, mida peetakse täna Itaalias Sitsiilia saare peamiseks meresadamaks..
Tol ajal oli Syracuse üks linnadest, mis koosnes nn Magna Greciast, mis oli Kreeka päritolu asustajate ruum Itaalia ja Sitsiilia poolsaare lõunapiirkonda..
Archimedese ema kohta puuduvad teadaolevad faktid. Isaga seoses on teada, et seda nimetati Phidiaseks ja et ta oli pühendunud astronoomiale. See tema isa teave on teada tänu raamatu fragmendile Liiva loendur, kirjutanud Archimedes, kus ta mainib oma isa nime.
Heraklides, kes oli kreeka filosoof ja astronoom, oli väga armastatud Archimedest ja isegi kirjutas temast elulugu. See dokument ei ole siiski säilinud, nii et kogu selles sisalduv teave ei ole teada.
Teisest küljest märkis ajaloolane, filosoof ja biograaf Plutarco oma raamatus pealkirjaga Parallel Lives, et Archimedesel oli suhete Hiero II-ga, türannaga, kes oli Siracuses alates 26. märtsist eKr..
Koolitus
Tänu vähesele teabele, mis meil on Archimedese kohta, ei tea me kindlalt, kus ta sai esimese koolituse.
Siiski on erinevad historiograafid leidnud, et on suur võimalus, et Archimedes õppis Aleksandria piirkonnas, mis oli kõige olulisem Kreeka kultuuri- ja õppekeskus selles piirkonnas..
Seda eeldust toetab Kreeka ajaloolase Diodoro Sículo pakutud teave, kes märkis, et Archimedes on tõenäoliselt õppinud Aleksandrias.
Lisaks mainib Archimedes paljudes oma töödes teisi teadlasi sellest ajast, mille töö oli koondunud Aleksandriasse, mistõttu võib eeldada, et ta tegelikult selles linnas areneb.
Mõned isiksused, kellega arvatakse, et Archimedes on Aleksandriast suhelnud, on geograaf, matemaatik ja astronoom Eratosthenes of Cyrene ning matemaatik ja astronoom Conon de Sanos.
Pere motivatsioon
Teisest küljest, asjaolu, et Archimedese isa oli astronoom, võib olla oluliselt mõjutanud tema hiljem näidatud kalduvusi, sest hiljem ja noores eas oli eriline atraktsioon selles valdkonnas. teadused.
Pärast oma aega Aleksandrias hinnatakse, et Archimedes naasis Syracusesse.
Teaduslik töö
Pärast Siracusesse naasmist hakkas Archimedes välja töötama erinevaid esemeid, mis võitsid talle kiiresti selle linna elanike seas teatud populaarsuse. Sel perioodil andis ta end täielikult teaduslikule tööle, tootis erinevaid leiutisi ja tegi mitmeid matemaatilisi mõisteid, mis olid oma ajaga väga arenenud.
Näiteks, kui ta pühendas tahkete ja lame numbrite omaduste uurimisele, tuli ta välja integraalse ja diferentsiaalse arvutusega seotud kontseptsioonidega, mis töötati välja hiljem.
Samuti määras Archimedes kindlaks, et keraga seotud maht vastab kahekordsele selle silindri suurusele, ja see oli see, kes leiutas komposiitrulli, tuginedes tema avastustele hoova õiguse kohta..
Konflikt Siracusas
Aastal 213 eKr, sisenesid Rooma sõdurid Syracuse linna ja ümbritsesid oma asunikke, et nad loobuksid.
Seda tegevust juhtis sõjavägi ja kreeka poliitik Marco Claudio Marcelo Teise Punase sõja raames. Hiljem tuntakse seda Rooma mõõkana, sest see lõppes Siracusa vallutamisega.
Kaks aastat kestnud konflikti keskel võitlesid Syracuse elanikud julguse ja raevuga roomlaste vastu ning Archimedes mängis väga olulist rolli, arvestades, et ta pühendas romade lüüasaamisele suunatud vahendite ja vahendite loomisele..
Lõpuks võttis Marco Claudio Marcelo Syracuse linna. Enne Archimedese suurt intellektuaalsust käskis Marcelo neid vigastada ega tappa. Kuid Archimedes tapeti Rooma sõduri käes.
Surm
Archimedes suri aastal 212 eKr. Rohkem kui 130 aastat pärast tema surma oli 137aastal eKr. Kirjanik, poliitik ja filosoof Marco Tulio Cicero Rooma halduses ning tahtis leida Archimedese hauda..
See ülesanne ei olnud kerge, sest Cicero ei suutnud leida kedagi, kes täpset kohta märkaks. Lõpuks sai ta siiski Agrigento uksele ja kahetsusväärsetele tingimustele väga lähedal.
Cicero puhastas hauda ja avastas, et see on kirjutatud silindri sees oleva sfääriga, viidates avastusele, mida Archimedes mõnda aega tagasi tegi..
Versioonid tema surma kohta
Esimene versioon
Üks versioonidest ütleb, et Archimedes oli matemaatilise probleemi lahendamisel kesksel kohal, kui ta oli Rooma sõduri poole pöördunud. On öeldud, et Archimedes oleks võinud teda mõnda aega probleemi lahendada, nii et sõdur oleks teda tapnud.
Teine versioon
Teine versioon on sarnane esimesele versioonile. Arvestades, et Archimedes lahendas matemaatika probleemi, kui linn võttis.
Rooma sõdur sisenes oma ühendisse ja käskis teda kohtuda Marceloga ning Archimedes vastas, et ta peab lahendama probleemi, millega ta esimesena töötas. Sõdur sai selle vastuse tagajärjel häiritud ja tappis.
Kolmas versioon
See hüpotees näitab, et Archimedes oli käes suur matemaatikale iseloomulike instrumentide mitmekesisus. Siis nägi sõdur teda ja ta arvas, et tal võib olla väärtuslikke esemeid, nii et ta tappis ta.
Neljas versioon
See versioon illustreerib, et Archimedes oli kaldu maapinna lähedal, kaaludes plaane, mida ta õppis. Ilmselt tuli taga Rooma sõdur ja ta ei teadnud, et see oli Archimedes.
Archimedese teaduslik panus
Archimedese põhimõte
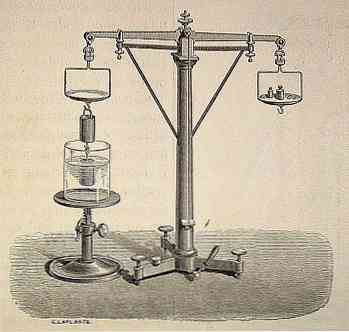
Tänapäeva teadus peab Archimedese põhimõtet üheks iidse ajastu üheks olulisemaks pärandiks.
Kogu ajaloo jooksul ja suuliselt on teatatud, et Archimedes avastas ta juhuslikult tänu King Hieronile, kes oli tellinud, et näha, kas tema poolt toodetud kuldkroon oli tehtud ainult kuldiks puhas ega sisaldanud ühtegi muud metalli. Ma pidin selle läbi viima ilma kroonit hävitamata.
On öeldud, et kui Archimedes mõtiskles, kuidas seda probleemi lahendada, otsustas ta vanni minna ja vannisse sisenedes sai ta aru, et vesi tõusis sellesse, kui ta endasse pani..
Sel moel avastab ta teadusliku põhimõtte, et "iga keha, mis on täielikult või osaliselt vees (vedelik või gaas) uputatud, saab ülespoole suunatud tõuke, mis on võrdne objekti poolt väljatõmmatud vedeliku massiga"..
See põhimõte tähendab, et vedelikud avaldavad tõukejõudu, mis tõuseb ülespoole mis tahes nendesse asetatud esemesse, ning et selle survet avaldava jõu kogus on võrdne veealuse keha poolt nihutatud vedeliku massiga, sõltumata selle kaalust..
Selle põhimõtte selgitus kirjeldab flotatsiooni nähtust ja leiab selle selle Ujuvorganite kohta.
Archimedese põhimõtet on oluliselt järgitud massiliseks kasutamiseks mõeldud objektide, näiteks allveelaevade, laevade, päästevestijate ja õhupallide ujumiseks..
Mehaaniline meetod
Veel üks Archimedesi kõige olulisem panus teadusse oli puhtalt mehaanilise, st tehnilise meetodi kaasamine geomeetriliste probleemide põhjendamisse ja argumenteerimisse, mis tähendas enneolematut viisi selle aja probleemide lahendamiseks..
Archimedese kontekstis peeti geomeetriaid eranditult teoreetiliseks teaduseks ja üldine asi oli see, et puhas matemaatika on langenud teiste praktiliste teaduste poole, kus selle põhimõtteid saaks rakendada..
Sel põhjusel peetakse seda tänapäeval mehaanika kui teadusliku distsipliini eelkäijaks.
Kirjutamisel, kus matemaatik avaldab uue meetodi oma sõbrale Eratosthenesile, näitab see, et see võimaldab lahendada matemaatika küsimusi mehaanika kaudu ja et geomeetrilise teoreemi tutvustamine on mõnevõrra lihtsam, kui see on juba omada mõningaid eelnevaid praktilisi teadmisi, et kui teil pole sellest mingit ideed.
See uus Archimedese poolt läbiviidud uurimise meetod muutuks kaasaegse teadusliku meetodi mitteametliku avastamise ja hüpoteesi koostamise eelkäijaks..
Kangi õiguse selgitus
Kuigi hoob on lihtne masin, mida kasutati palju varem kui Archimedes, oli see see, kes sõnastas põhimõtte, mis selgitab oma tööd oma traktaatides tasapinnas..
Selle seaduse sõnastamisel kehtestab Archimedes põhimõtted, mis kirjeldavad kangi erinevat käitumist kahe keha paigutamisel, sõltuvalt selle kaalust ja kaugusest tugipunktist.
Sel viisil juhib ta tähelepanu asjaolule, et kaks keha, mida on võimalik mõõta (proportsionaalne), mis asuvad kangil, on tasakaalus, kui nad on nende kaaluga pöördvõrdelises kauguses..
Samamoodi teevad mõõtmatud kehad (mida ei saa mõõta), kuid Archimedes oli seda seadust tõendatav ainult esimese tüübi kehadega..
Selle hoova põhimõtte sõnastus on hea näide mehaanilise meetodi rakendamisest, sest vastavalt sellele selgitab see Dositeole suunatud kirjas, et see avastati esimesel hetkel mehaanika meetodite abil, mis praktikas rakendati..
Hiljem sõnastas ta need geomeetria meetodite abil (teoreetiline). Sellest keha katsetamisest eraldati ka raskuskeskme mõiste.
Teaduslikuks demonstratsiooniks vajaliku või ammendava meetodi väljatöötamine
Ammendumine on meetod, mida kasutatakse geomeetrias, mis koosneb geomeetriliste arvude lähendamisest, mille pindala on pealkirja ja piirjoonte abil teada teisele, kelle pindala on teada..
Kuigi Archimedes ei olnud selle meetodi looja, töötas ta selle meisterlikult välja, suutes selle abil arvutada Pi täpse väärtuse..
Archimedes, kasutades väljatõmbamismeetodit, kirjutatud ja piiritletud kuusnurkade läbimõõduga 1, vähendades absurdi vahe kuuskantide ja ümbermõõdu pindala vahel.
Selleks lõhkus ta kuusnurkadeks, luues kuni 16 külje poligoneid, nagu on näidatud eelmisel joonisel.
Nii jõudis ta täpsustama, et pi (väärtus ringi pikkuse ja selle läbimõõdu vahel) on väärtuste 3.14084507 ... ja 3.14285714 vahel. .
Archimedes kasutas meisterlikult exhaucióni meetodit, sest mitte ainult ei suutnud piigi väärtuse arvutamist veamääraga üsna madalale ja seega soovida, vaid ka seetõttu, et Pi on irratsionaalne arv läbi see meetod ja saadud tulemused panid aluse, mis idanevad lõpmatusse arvutussüsteemi, ja hiljem, kaasaegses integraalses kalkulaatoris..
Ringi mõõt
Ringi ala kindlaksmääramiseks kasutas Archimedes meetodit, mis seisnes ringi joonistamiseks vajaliku ruudu joonistamises.
Teades, et ruudu pindala oli selle külgede summa ja et ringi pindala oli suurem, hakkas ta töötama lähenduste saamiseks. Seda tegi ta, asendades ruudu 6-poolse polügooniga ja töötades seejärel keerukamate hulknurkadega.
Archimedes oli esimene matemaatik ajaloos, et läheneda arvule Pi tõsiselt.
Sfääride ja silindrite geomeetria
Üheksast Archimedese töö matemaatikas ja füüsikas koostatud kohtumisest on kaks sfääride ja silindrite geomeetriat..
Selles töös käsitletakse selle kindlaksmääramist, et ükskõik millise raadiusesfääri pind on neli korda suurem kui selle suurim ring ning et kera maht on kaks kolmandikku selle silindri mahust, kus see on kirjutatud.
Leiutised
Odomeeter
Tuntud ka kui kilomeetreid, see oli selle kuulsa inimese leiutis.
See seade ehitati rattapõhimõtte alusel, mis aktiveerib käigud, mis võimaldavad arvutada läbitud vahemaa..
Sama põhimõtte kohaselt kavandas Archimedes sõja- ja tsiviilotstarbel mitmesuguseid mõõtureid.
Esimene planetaarium
Paljude klassikaliste kirjanike, nagu Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico ja Lactantius, ütluste põhjal omistavad paljud teadlased nüüd Archimedesele esimese algelise planetaariumi loomise..
See on mehhanism, mis koosneb mitmetest "sfääridest", mis suutsid jäljendada planeetide liikumist. Seni ei ole selle mehhanismi üksikasjad teada.
Cicero sõnul olid Archimedese ehitatud planetaariumid kaks. Ühes neist oli esindatud maa ja selle lähedal asuvad erinevad tähtkujud.
Teises, üksiku pööramisega, tegid päike, kuu ja planeedid iseseisvaid liikumisi fikseeritud tähtedega võrreldes samal viisil, nagu nad tegid reaalsel päeval. Viimases võib täheldada ka kuu järjestikuseid faase ja pimendusi.
Archimedese kruvi
Archimedese kruvi on seade, mida kasutatakse vee transportimiseks alt ülespoole läbi kalle, kasutades toru või silindrit.
Kreeka ajaloolase Diodoro sõnul lihtsustati tänu sellele leiutisele iidse Egiptuse Niiluse jõe ääres asuvate viljakate maade niisutamist, kuna traditsioonilised vahendid nõudsid tohutut füüsilist pingutust, mis ammendas töötajad..
Kasutatud silindril on sama pikkusega kruvi, mis hoiab omavahel ühendatud sõukruvide või uimede süsteemi, mis teostavad pöörleva hoova abil käsitsi liikuvat pöörlevat liikumist.
Sel moel õnnestub helikidel suruda mis tahes ainet alt üles, moodustades teatud lõpmatu ahela.
Archimedese küünis
Archimedese küünis või raua käsi, nagu see ka on teada, oli üks kõige hirmuäratavamaid relvi, mille see matemaatik lõi, muutudes Sitsiilia kaitseks Rooma sissetungide jaoks kõige olulisemaks..
Drexeli ülikooli professorite Chris Rorres'i (matemaatika osakond) ja Harry Harrise (tsiviilehituse ja arhitektuuri osakond) uuringute kohaselt oli hoova külge kinnitatud suur hoob. selle abil riputatud kett.
Kangi kaudu manipuleeriti konksu nii, et see langes vaenlase laeva peale ja selle eesmärk oli haakida see üles ja tõsta see sellisel määral, et selle vabastamisel oleks võimalik seda täielikult ümber pöörata või kaldale kividega tabada..
Rorres ja Harris esitlesid sümpoosionil "Masinad ja antiikse struktuurid" (2001), mis on selle artefakti miniatuurne esitus pealkirjaga "Suur sõjamasin: Archimedese raudraami ehitamine ja käitamine"
Selle töö realiseerimiseks toetusid nad vanade ajaloolaste Polibio, Plutarco ja Tito Livio argumentidele..
Viited
- ASSIS, A. (2008). Archimedes, raskuskese ja esimene mehaanika seadus [online]. Juurdepääs 10. juunil 2017 bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [online]. Juurdepääs 9. juunil 2015 World Wide Web'is: books.google.co.ve/books.
- MOLINA, A. (2008). Siracusa Archimedese uurimismeetod: intuitsioon, mehaanika ja võimendamine [online]. Juurdepääs 10. juunil 2017 World Wide Webproduccioncientifica.luz.edu.
- O'CONNOR, J. & ROBERTSON, R. (1999). Syracuse Archimedes [online]. Juurdepääs 9.06.2017 aadressil history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimedes: tema elu, tööd ja kaasaegse matemaatika toetused [online]. Välja otsitud 9. juunil 2017 kell lfunes.uniandes.edu.co.
- QUINN, L. (2005). Syracuse Archimedes [online]. Juurdepääs 9. juunini 2017 aadressil math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). Võimas sõjamasin: Archimedese raudkäsu ehitamine ja käitamine. Välja otsitud 10. juunil 2017 kell cs.drexel.edu.
- VITE, L. (2014). Archimedese põhimõte [online]. Välja otsitud 10. juunil 2017 kell repository.uaeh.edu.mx.


