Colinear süsteem ja näited
The kolinäärsed vektorid Need on üks olemasolevatest vektoritest. See on nende vektorite kohta, mis on samas suunas või tegevussuunda. See tähendab järgmist: kaks või enam vektorit on kollinaarsed, kui need on paigutatud üksteisega paralleelseteks sirgjateks.
Vektor määratletakse kui kehale rakendatud kogust, mida iseloomustab suund, mõte ja skaala. Vektorid võivad olla tasapinnas või ruumis ja need võivad olla erinevat tüüpi: kolinäärsed vektorid, samaaegsed vektorid ja paralleelsed vektorid.

Indeks
- 1 kolinaalsed vektorid
- 2 Omadused
- 2.1 Näide 1
- 2.2 Näide 2
- 2.3 Näide 1
- 3 Collinear vektorisüsteem
- 3.1. Kollektiivsed vektorid, millel on vastupidised tunded
- 3.2 Sama mõttega kollektiivsed vektorid
- 3.3 Kollektiivsed vektorid, millel on võrdsed suurused ja vastassuunalised tunded
- 4 Kollektiivsete ja samaaegsete vektorite erinevus
- 5 Viited
Kollisioonivektorid
Vektorid on kollisioonid, kui ühe toimimisviis on täpselt sama, mis kõigi teiste vektorite tegevussuund, olenemata iga vektori suurusest ja mõttest.
Vektoreid kasutatakse esindustena erinevates valdkondades nagu matemaatika, füüsika, algebra ja ka geomeetria, kus vektorid on kollektiivsed ainult siis, kui nende suund on sama, sõltumata sellest, kas nende tähendus ei ole.
Omadused
- Kaks või enam vektorit on kollektiivsed, kui koordinaatide suhe on võrdne.
Näide 1
Meil on vektorid m = m_x; m_y ja n = n_x; n_y. Need on kollektiivsed, kui:
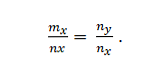
Näide 2
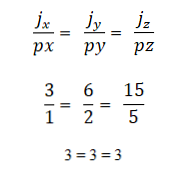
- Kaks või enam vektorit on kollektiivsed, kui toode või vektori korrutamine on võrdne nulliga (0). Seda seetõttu, et koordinaatsüsteemis on iga vektorit iseloomustatud vastavate koordinaatidega ja kui need on üksteisega proportsionaalsed, on vektorid kollinaarsed. Seda väljendatakse järgmiselt:
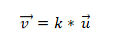
Näide 1
Meil on vektorid a = (10, 5) ja b = (6, 3). Et määrata kindlaks, kas need on kollektiivsed, kasutatakse determinantide teooriat, mis määrab risttoodete võrdsuse. Nii peate:
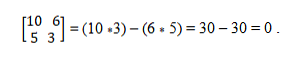
Koliinia vektori süsteem
Kolinäärsed vektorid on esitatud graafiliselt, kasutades nende suunda ja tähendust, arvestades, et nad peavad läbima rakenduskoha ja mooduli, mis on kindel skaala või pikkus.
Kollisioonivektorite süsteem moodustub siis, kui kaks või enam vektorit toimivad objektile või kehale, esindades jõudu ja toimides samas suunas.
Näiteks, kui kehale rakendatakse kahte kollinaarset jõudu, sõltub nende tulemus ainult sellest, millises suunas nad tegutsevad. On kolm juhtumit, mis on:
Kollisioonivektorid, millel on vastupidised tunded
Kahe kollektiivse vektori tulemus on võrdne nende summaga:
R = Σ F = F1 + F2.
Näide
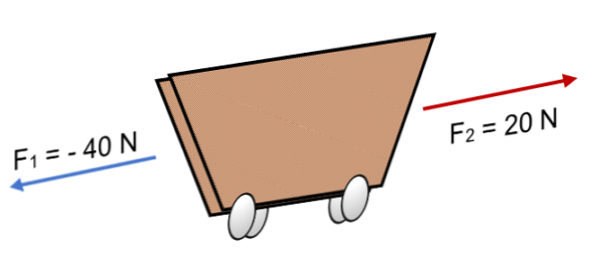
Kui kaks jõudu tegutsevad ostukorvi F1 = 40 N ja F2 = 20 N vastupidises suunas (nagu näidatud joonisel), on tulemus:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
Kollektiivsed vektorid sama tähendusega
Saadud jõu suurus on võrdne kollinaarsete vektorite summaga:
R = Σ F = F1 + F2.
Näide
Kui kaks jõudu tegutsevad ostukorvi F1 = 35 N ja F2 = 55 N samas suunas (nagu näidatud pildil), on tulemus:
R = Σ F = 35 N + 55N.
R = 90 N.
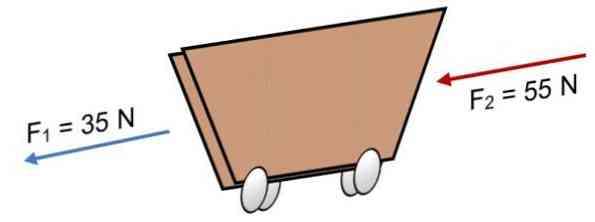
Positiivne tulemus näitab, et kollinaarsed vektorid toimivad vasakule.
Kollektiivsed vektorid, millel on võrdsed suurused ja vastupidised meeli
Kahe kollektiivse vektori tulemus on võrdne kollinaarsete vektorite summaga:
R = Σ F = F1 + F2.
Kuna jõud on sama suur, kuid vastupidises suunas, siis on üks positiivne ja teine negatiivne, kui kahe jõu lisamisel on tulemuseks võrdne nulliga.
Näide
Kui kaks jõudu tegutsevad ostukorvi F1 = -7 N ja F2 = 7 N, mis on sama suurusega, kuid vastupidises suunas (nagu näidatud joonisel), on tulemus:
R = ΣF = (-7 N) + 7N.
R = 0.
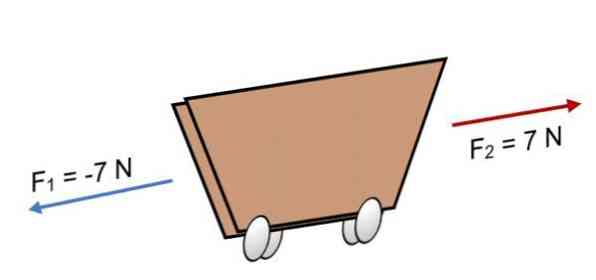
Kuna tulemus on võrdne 0-ga, tähendab see, et vektorid on üksteise suhtes tasakaalus ja seetõttu on keha tasakaalus või puhkeasendis (see ei liigu).
Kollektiivsete ja samaaegsete vektorite erinevus
Kollisioonivektorid on iseloomustatud sellega, et neil on samas suunas sama suund või kuna need on joonega paralleelsed; see tähendab, et nad on vektorid, mis on otsesed paralleelsed jooned.
Teisest küljest on samaaegsed vektorid defineeritud, sest nad on erinevates tegevussuundades, mis on kinnitatud ühes punktis.
Teisisõnu, neil on sama päritolukoht või saabumine - olenemata nende moodulist, suunast või suunast -, moodustades nende vahel nurga.
Samaaegsete vektorite süsteemid lahendatakse matemaatiliste meetodite või graafikutega, mis on jõudude rööpküliku meetod ja jõudude hulknurga meetod. Nende kaudu määratakse tulemuseks oleva vektori väärtus, mis näitab suunda, millesse keha liigub.
Põhimõtteliselt on peamine erinevus koloonia vektorite ja samaaegsete vektorite vahel tegevussuund, milles nad toimivad: kollinaarsed toimivad samas reas, samal ajal kui samaaegsed on erinevad.
See tähendab, et kollektiivsed vektorid toimivad ühes tasapinnas, "X" või "Y"; ja samaaegne tegu mõlemas lennukis, alates samast punktist.
Kollisioonivektorid ei ole ühel hetkel, nagu samaaegsed, sest nad on üksteisega paralleelsed.
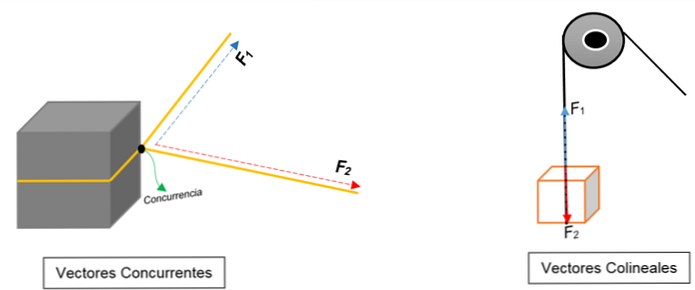
Vasakul pildil on näha plokk. See on seotud köie ja sõlm jagab selle kaheks; erinevate suundade ja erinevate jõudude suunas tõmmates liigub plokk sama suuna suunas.
Esitatakse kaks vektorit, mis vastavad punktile (plokk), sõltumata nende moodulist, mõttest või suunast.
Selle asemel kuvatakse paremal pildil rihm, mis tõstab kasti. Köis on tegevussuund; tõmmates toimivad kaks jõudu (vektorid): üks pingetugevus (blokeerimisel) ja teine jõud, see, mis avaldab ploki kaalu. Mõlemal on sama suund, kuid vastupidises suunas; ei nõustu ühe punktiga.
Viited
- Estalella, J. J. (1988). Vektori analüüs. 1. köide.
- Gupta, A. (s.f.). Tata McGraw-Hill Haridus.
- Jin Ho Kwak, S. H. (2015). Lineaarne algebra. Springer Science & Business Media.
- Montiel, H. P. (2000). Füüsika 1 tehnoloogilise küpsustunnistuse jaoks. Patria Toimetusgrupp.
- Santiago Burbano de Ercilla, C. G. (2003). Üldine füüsika Toimetaja Tebar.
- Sinha, K. (s.f.). Matemaatika tekstiraamat XII köide. Rastogi väljaanded.


